ANALISA CURAH HUJAN RENCANA
ABSTRAK
Dalam Ilmu Geografi, curah hujan
merupakan unsur terpenting yang wajib dipelajari oleh mahasiswa baik pesebaran
dan penghitungannya. Peran hujan sangat penting dalam siklus Hidrologi . Hujan
berasal dari kondensasi uap air yang jatuh kembali ke permukaan bumi sehingga
dalam analisis siklus Hidrologi curah hujan selalu diperhitungkan.
Sebagai negara yang terletak di garis khatulistiwa, Indonesia memiliki musim kemarau dan penghujan yang dikatakan seimbang. Adanya dua jenis musim ini memberi pengaruh terhadap kelangsungan hidup berbagai makhluk hidup di Indonesia. Oleh sebab itu, pentingnya mengerti dan memahami kondisi curah hujan setiap musim sangat diperlukan agar kegiatan berjalan lancar, khususnya dalam bidang pangan.
Sebagai negara yang terletak di garis khatulistiwa, Indonesia memiliki musim kemarau dan penghujan yang dikatakan seimbang. Adanya dua jenis musim ini memberi pengaruh terhadap kelangsungan hidup berbagai makhluk hidup di Indonesia. Oleh sebab itu, pentingnya mengerti dan memahami kondisi curah hujan setiap musim sangat diperlukan agar kegiatan berjalan lancar, khususnya dalam bidang pangan.
PENDAHULUAN
Curah hujan adalah
jumlah air yang jatuh pada periode tertentu. Pengukurannya dilakukan dengan
satuan tinggi diatas permukaan tanah horizontal yang diasumsikan tidak terjadi
penguapan atau infiltrasi, run off, atau evaporasi.
Secara lebih rinci, curah hujan
memiliki pengertian sebagai air hujan dengan ketinggian tertentu yang terkumpul
menjadi satu dalam penakar hujan, tidak meresap, tidak mengali dan tidak
menyerap (utuh dan tidak mengalami kebocoran).
Tinggi air yang jatuh
dinyatakan dalam satuan milimiter. Contohnya adalah curah hujan 1 milimeter
merupakan ketinggian air hujan dalam luasan penampung 1 meter persegi. Jika
dihitung, maka dalam 1 meter persegi akan terkumpul 1 liter air.
Hujan rencana adalah hujan harian maksimum yang akan digunakan untuk menghitung intensitas hujan. Untuk mendapatkan curah hujan rancangan (Rt) dilakukan melalui analisa frekuensi antara lain :
ANALISA FREKUENSI CURAH HUJAN
Parameter Statistik
· Nilai rata-rata
Dimana :
X = nilai rata-rata curah hujan
Xi = nilai pengukuran dari suatu curah hujan ke-i
n = jumlah data curah hujan
· Standar deviasi

Dimana :
Sd = standar deviasi curah hujan
X = nilai rata-rata curah hujan
Xi = nilai pengukuran dari suatu curah hujan ke-i
n = jumlah data curah hujan
· Koefisien variasi
Dimana :
Cv = koefisien variasi curah hujan
Sd = standar deviasi curah hujan
X = nilai rata-rata curah hujan
· Koefisien kemencengan
Dimana :
Cs = koefisien kemencengan curah hujan
Sd = standar deviasi dari sampel curah hujan
X = nilai rata-rata dari data sampel curah hujan
n = jumlah data curah hujan
· Koefisien kurtosis
Dimana :
Ck = koefisien kurtosis curah hujan
n = jumlah data curah hujan
Xi = curah hujan ke i
X = nilai rata-rata dari data sampel
fi = nilai frekuensi variat ke i
Sd = standar deviasi
Penentuan jenis sebaran yang akan
digunakan untuk analisis frekuensi dapat dipakai beberapa cara sebagai berikut.
a.
Sebaran Gumbel Tipe I
Untuk menghitung curah hujan
rencana dengan metode sebaran Gumbel Tipe I digunakan persamaan distribusi
frekuensi empiris sebagai berikut (CD.Soemarto, 1999) :
Hubungan antara periode ulang T dengan YT dapat
dihitung dengan rumus :
untuk T ≥ 20, maka : Y
= ln T
Dimana :
XT =
nilai hujan rencana dengan data ukur T tahun.
X = nilai
rata-rata hujan
S = standar
deviasi (simpangan baku)
YT =
nilai reduksi variat ( reduced variate ) dari variabel yang diharapkan terjadi pada periode ulang T
tahun. Tabel 3.3.
Yn = nilai
rata-rata dari reduksi variat (reduce mean) nilainya
tergantung dari jumlah data (n). Tabel 3.2.
Sn = deviasi
standar dari reduksi variat (reduced standart deviation) nilainya tergantung dari jumlah
data (n). Tabel 2.3.
Tabel 3.2. Reduced
mean (Yn) dan Reduced Standard Deviation (Sn) untuk Metode Sebaran Gumbel Tipe
I
(Sumber: Bambang Triatmodjo. 2010)
Tabel 3.3. Reduced
Variate (YT) untuk
Metode Sebaran
Gumbel I
b.
Sebaran
Log-Pearson III
Metode Log-Pearson tipe III model matematik dengan persamaan sebagai berikut (CD.Soemarto, 1999):
Dimana :
Y = nilai logaritmik dari X atau log (X)
X = data curah hujan
ȳ = rata-rata hitung (lebih baik rata-rata
geometrik) nilai Y
S =
deviasi standar nilai Y
K = karakteristik distribusi peluang Log-Pearson
tipe III ( Tabel 2.5)
Tabel
3.4 Harga K untuk Metode Sebaran Log-Pearson III
DAFTAR PUSTAKA
Soemarto, CD, 1999. Hidrologi Teknik edisi dua.
Jakarta:Airlangga
Anonim, 2019. Curah Hujan - Pengertian, Jenis, dan Metode Perhitungan. https://rimbakita.com/curah-hujan/


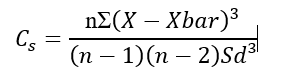








Tidak ada komentar:
Posting Komentar